Delaunay Triangulation

한국어로 들로니 삼각분할 이라고 하며 이번에 들로니 그래프에 대해 간단하게 정리해보자.

 

먼저 들로니 삼각분할은 그래프가 있을때, 삼각형을 만드는데 각각의 삼각형들은 본인들 세 점을 제외한 다른 점을 포함하지 않게끔 삼각형을 만들어 분할하는 것을 의미한다.

 

이것을 가지고 어떤 특정 점에서 가장 가까운 거리에 있는 위치를 찾을 수 있다.

 

이걸 응용하여 들로니 그래프가 있을때, cycle을 이루는 정점들의 집합을 바탕으로 모든 정점들이 가중치 w이하에서 모든 정점을 커버하는지 확인해 볼것이다. 즉, 모든 정점에서 cycle을 이루는 정점으로 가중치 w이하의 값으로 연결되는지 확인하는 과정이다.

 

먼저 들로니 그래프를 구현하는 python 코드이다. 본 글의 목적은 들로니 그래프가 구현되어 있을때, 모든 정점이 cycle을 이루는 가장 가까운 정점으로 가중치 w안에 존재하는지 확인하는것이다.

 

import sys
import networkx as nx
import math
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
import numpy as np
 
def euclidean( s, d ) :
    if( (s < 0) or (d < 0) or (s > len(P)) or (d > len(P)) ) :
        print("invalid query")
        sys.exit()
    xdiff = P[s][0]-P[d][0]
    ydiff = P[s][1]-P[d][1]
    return round(math.sqrt(xdiff**2+ydiff**2),3)
# ============== end of euclidean() ==============
 
G = nx.Graph()  # Graph
N = 0            # The number of point
w0 = 0            # Threshold value ( vertex to cycle )
P = []          # Point [ [x1, y1], [x2, y2], ...]  list
C = []          # Cycle vertex [ v1, v2, .. ] list
C_sz = 0        # The number of Cycle vertex
C_length = 0    # The Length of Cycle
C_valid = 1     # Cycle validation
C_max_dist = 0  # The longest distance (v)->(cycle)
C_max_v = 0     # longest distance vertex
C_max_E = []    # longest distance path
CE_IN = []      # Cycle edge in DG
CE_OUT = []     # Cycle edge out of DG
 
city_f = open("city-100.txt",'r')
cycle_f = open("citycycle-100.txt", 'r')
 
 
# Read cycle data and check
C_sz = int(cycle_f.readline())
C = list(map(int, cycle_f.readline().split()))
if( C[0] != C[-1] or len(C[1:]) != len(set(C[1:])) ) :
    print("invalid cycle input")
    sys.exit()
 
 
# Read point data and checkpyscripter 줄번호
N, w0 = map(int, city_f.readline().split())
for line in city_f :
    p = list(map(int, line.split()))
    if( p in P ) :
        print( "invalid point input")
        sys.exit()
    else : P.append( p )
 
 
### 추가된 부분 ( edge 정보 파일 출력 )
dgfile = open("city-dg.txt",'w')
 
# Add node & edge to G ( based on Delaunay Graph )
tri = Delaunay(P)
for i in range(1, N+1) :
    G.add_node( i, pos=P[i-1])
for t in tri.simplices.copy() :
    G.add_edge( t[0]+1, t[1]+1, weight=euclidean(t[0], t[1]))
    G.add_edge( t[1]+1, t[2]+1, weight=euclidean(t[1], t[2]))
    G.add_edge( t[0]+1, t[2]+1, weight=euclidean(t[0], t[2]))
 
    ### 추가된 부분( 위 3줄을 파일로 출력 )
    print(t[0]+1, t[1]+1, euclidean(t[0], t[1]), file=dgfile)
    print(t[1]+1, t[2]+1, euclidean(t[1], t[2]), file=dgfile)
    print(t[0]+1, t[2]+1, euclidean(t[0], t[2]), file=dgfile)
 
dgfile.close()
 
# Cycle check
for i in range( len(C)-1 ) :
    e = [C[i], C[i+1]]
    if( e in G.edges() ): # cycle edge on DG
        CE_IN.append( e )
    else :
        CE_OUT.append( e )
    C_length += euclidean( C[i]-1, C[i+1]-1 )
if( len(CE_OUT) > 0 ) : C_valid = 0
 
# Calculate ditance between vertices and cycle
path = nx.johnson(G, weight='weight')   # or nx.all_pairs_dijkstra_path_length(G)
print("1. All Shortest Path (v-->cycle)")
print("vertex -- cycle_vertex ==> distance [path]")
for i in range( 1, len(P)+1 ) :
    if( i in C ) : continue
    else:
        min_dist = 1000*1000
        min_idx = 0
        for j in C :
            cur_dist = 0
            for k in range( len(path[i][j])-1 ) :
                cur_dist += G[path[i][j][k]][path[i][j][k+1]]['weight']
            if( cur_dist < min_dist ) :
                min_dist = cur_dist
                min_idx = j
        print( "   ", i, "--" , min_idx, "==>", round(min_dist,3), path[i][min_idx] )
        if( C_max_dist < min_dist ) :
            C_max_dist = min_dist
            C_max_v = (i, min_idx)
if( C_max_dist > w0 ) :
    C_valid = 0
max_path = path[C_max_v[0]][C_max_v[1]]
for i in range( len(max_path)-1 ) :
    C_max_E.append( [max_path[i], max_path[i+1]] )
 
# Report
print( "\n 2. Longest Distance is", C_max_v, "==>", C_max_dist)
print( "\n 3. Cycle Length is", C_length )
if( C_valid == 0 ) : print( "\n --> Wrong cycle answer!" )
else :               print( "\n --> Correct cycle answer!")
 
# Draw Delaunay Graph and Cycle ========================================================================
pos=nx.get_node_attributes(G,'pos')
nx.draw_networkx_nodes (G, pos, node_size=300, alpha=0.7, node_color='skyblue')
nx.draw_networkx_nodes (G, pos, node_size=300, nodelist=C, node_color='r')
nx.draw_networkx_nodes (G, pos, node_size=300, nodelist=[C_max_v[0]], node_color='orange')
nx.draw_networkx_edges (G, pos, width=0.5)
nx.draw_networkx_edges (G, pos, edgelist=CE_IN, width=3.0, alpha=0.6, style='dashed', edge_color='r') # Cycle edge on DG
nx.draw_networkx_edges (G, pos, edgelist=CE_OUT, width=3.0, alpha=0.6, style='dashed', edge_color='grey') # Cycle edge out of DG
nx.draw_networkx_edges (G, pos, edgelist=C_max_E, width=5.0, alpha=0.6, edge_color='orange') # longest distance
nx.draw_networkx_labels(G, pos, font_size=8, font_weight='bold' )
 
plt.tight_layout()
plt.subplots_adjust(left = 0, bottom = 0, right = 1, top = 1, hspace = 0, wspace = 0)
plt.show()
 

  

들로니 그래프의 샘플 코드이다. 패키지를 이용해 구현할 수 있다.

city-100.txt가 각 도시들의 위치와 가중치를 가지고 있는데 데이터이고 citycycle-100은 필자의 방법으로 cycle을 이루어야 하는 정점들의 집합을 가지는 데이터이다. 데이터는 공개하지 않는다.

citydg.txt는 만들어진 들로니 그래프를 텍스트파일로 추출하기위한 방법이다. 이제 얻어진 들로니 그래프의 데이터로 cycle을 구해보는 작업을 해보자.

 

이 문제는 명확한 정답이 존재하지 않으며 정확하지 않다. 먼저 필자는 2차원 평면으로 이해하여 (x,y) 좌표의 최대와 최소를 기반으로 각 거리의 중앙값을 활용하여 접근을 하였다. 아래 코드가 그 내용이다.

 

#include<stdlib.h>
#include<iostream>
#include<fstream>
#include<string.h>
#include<string>
#include<math.h>
#include<algorithm>
#include<stack>
#include<queue>
#include<set>
#include<iterator>
#include<deque>
#include<map>
 
using namespace std;
 
typedef struct node {
    int x = 0, y = 0;
}no;
 
vector<pair<int, float>> arr[500];
set<int> ss,ans;
int w0, N, xmax, xmin = 987654321, ymax, ymin = 987654321, k, visit[500], Lcur[500],chk;
float d[500][500] = { 0.0 },Long[500];
float xmid, ymid;
no ap[500];
//풀이 : bfs를 통해 가중치 이하의 방문 가능한 정점을 모두 체크
//-> 수정 : 최와각 노드 4개만 먼저 탐색 : x=min,y=min, x=max,y=max x=min,y=max x=max,y=min
// 구간을 4개 구간으로 나누어서 체크해야함 -> 최외각노드가 갈수 있는 노드를 무조건 포함하는 cycle을 만들도록
// 뽑아낸 노드를 bfs하고 가운데 노드를 bfs로 방문하면서 중복된 노드를 찾음.
// 그 vertex는 cycle의 노드라는 의미
// 해결할 부분 : 구한 cycle 노드가 최적인지 아닌지 판단, 시간복잡도 생각
 
void bfs(int a) { // 다익스트라를 통해 노드 a에서 w0이하의 방문가능한 정점 체크
    priority_queue<pair<float, int>> pq;
    vector<int> v;
    for (int i = 1; i <= N; i++) d[a][i] = 100000.0;
    d[a][a] = 0.0;
    pq.push({ 0.0,a });
    while (!pq.empty()) {
        int cur = pq.top().second;
        float dis = -pq.top().first;
        pq.pop();
        //cout << cur << "  " << dis << endl;
        if (dis > d[a][cur]) continue;
        for (int i = 0; i < arr[cur].size(); i++) {
            int ncur = arr[cur][i].first;
            float ndis = dis + arr[cur][i].second;
            if (ndis < d[a][ncur]) {
                if (ndis <= w0) {
                    v.push_back(ncur);
                    visit[ncur]++;
                    d[a][ncur] = ndis;
                    if (ndis > Long[a]) {
                        Long[a] = ndis;
                        Lcur[a] = ncur;
                    }// a노드에서 최대로 갈수 있는 노드를 저장
                    pq.push({ -d[a][ncur],ncur });
                }
            }
        }
    }
}
 
int main()
{
    int a = 0;
    ifstream input("city-dg.txt");
    ifstream input2("city-100.txt");
    while (!input2.eof()) {
        int n, m;
        if (a == 0) {
            a = 1;
            input2 >> n >> m;
            N = n, w0 = m;
            continue;
        }
        input2 >> n >> m;
        ap[a].x = n, ap[a].y = m;
        xmax = max(xmax, n);
        xmin = min(xmin, n);
        ymax = max(ymax, m);
        ymin = min(ymin, m);
        a++;
    }
    while (!input.eof()) {
        int n, m;
        float w;
        input >> n >> m >> w;
        arr[n].push_back({ m,w });
        arr[m].push_back({ n,w });
    }
    //DG그래프와 각 노드의 위치를 저장, 그래프에서 x,y위치의 최소값과 최대값을 저장
    for(int i=1;i<=N;i++) Long[a] = -987654321;
    xmid = float(xmax + xmin) / 2;
    ymid = float(ymax + ymin) / 2;
    // 그래프에대한 중간위치를 저장
    for (int i = 1; i <= N; i++) {
        if (xmin + 100 >= ap[i].x) ss.insert(i);
        if (ymin + 100 >= ap[i].y) ss.insert(i);
        if (xmax - 100 <= ap[i].x) ss.insert(i);
        if (ymax - 100 <= ap[i].y) ss.insert(i);
        if (xmid + 200 >= ap[i].x && xmid - 200 <= ap[i].x && ymid + 200 >= ap[i].y && ymid - 200 <= ap[i].y) ss.insert(i);    
    }
    // 최외각 위치의 노드와 가운데 위치한 노드들을 적절히 선택하여 set에 저장
    
    //cout << N << "  " << w0 << endl;
 
    float q= (xmid - xmin) / 2, w= xmid + (xmax - xmid) / 2, e= (ymid - ymin) / 2, r= ymid + (ymax - ymid) / 2;
    // 그래프의 가운데와 최외각 사이의 가운데 위치를 저장
    
    for (auto it = ss.begin(); it != ss.end(); it++) {
        bfs(*it);
        if (Lcur[*it] == 0) chk = 1;
        if(Lcur[*it] != 0) ans.insert(Lcur[*it]);
        memset(Long, 0, sizeof(Long));
    }
    // 최외각 노드들과 가운데 사이의 노드들을 다익스트라를 통해 탐색, Lcur에 각 노드에서 가장 멀리갈 수 있는 노드를 저장
    // 그 노드는 cycle을 이루어야 하는 노드
    // chk가 1이 되는값은 최외각 노드나 가운데 있는 노드가 해당 가중치에서 갈 수 있는 노드가 없으므로 오류이다.
    //bfs(33);
    //printf("%d ", Lcur[33]);
    for (int i = 1; i <= N; i++) {
        //printf("%d : %d\n", i, visit[i]);
        if (visit[i] > N / 25) {
            if (ap[i].x >= q && ap[i].x <= w && ap[i].y >= e - 100 && ap[i].y <= e + 100) {
                ans.insert(i);
            }
            else if (ap[i].x >= q && ap[i].x <= w && ap[i].y <= r+100 && ap[i].y >= r - 100) {
                ans.insert(i);
            }
            else if (ap[i].y >= e && ap[i].y <= r && ap[i].x >= q - 100 && ap[i].x <= q + 100) {
                ans.insert(i);
            }
            else if (ap[i].y >= e && ap[i].y <= r && ap[i].x <= w + 100 && ap[i].x >= w - 100) {
                ans.insert(i);
            }
        }
    } // 여러번을 방문가능하며 해당 조건을 만족하는 정점들 중 다음의 위치를 만족하는 노드들을 set에 저장
      // 이 노드들은 cycle을 이룰수 있는 노드들이며, 최외각 위치와 가운데 위치의 가운데 값들이다.
    cout << ans.size() << endl;
    for (auto it = ans.begin(); it != ans.end(); it++) {
        cout << *it << " ";
    }
    printf("\n\n%d", chk); 
    // ans의 크기가 만족가능한 가장 큰 cycle의 노드이며 이 노드들을 기준으로 cycle을 최적화하고 만들어야 함.
    return 0;
}

 

이렇게 적어도 cycle을 이루어야 하는 노드를 구하였다. 문제는 이 노드들이 cycle을 이루는지 확인을 하지 않는다. 노드들을 표시할 뿐, 경로상 있는지 없는지 cycle을 이루는지 확인이 필요한 코드이다.

 

여기서 얻은 결과를 바탕으로 python 코드의 들로니 그래프에 적용하면 아래의 결과를 얻을 수 있다.

 

 

 

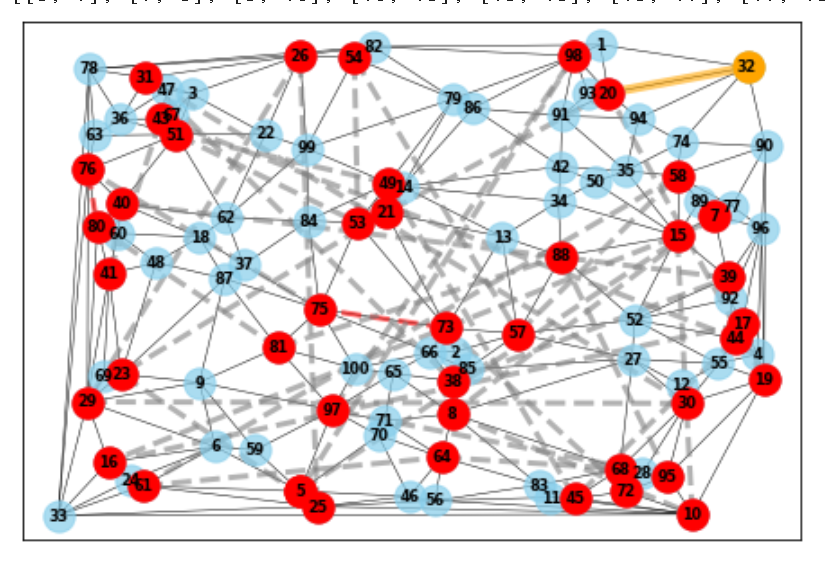
우선 들로니 그래프가 잘 그려져 있으며 빨간색 정점이 cycle에 속하는 정점이다. 노란색은 가중치가 가장 긴 노드사이의 edge를 나타낸다.

점선은 각 노드들이 연결된것을 의미하는데 현재 cycle로 지정하지 않고 노드의 오름차순으로 되어있기때문에 점선이 중구난방으로 이어져 있다. 연결된 노드끼리와의 탐색을 통해 cycle을 만드는 과정이 필요하다.

 

Reference

http://www.secmem.org/blog/2019/01/11/Deluanay_Triangulation/

https://darkpgmr.tistory.com/96