본 내용은 아래의 출처에서 본것이고 허락을 맡고 포스트한다.
출처 : https://talkingaboutme.tistory.com/category/About%20Study/Compiler
이때까지 정규 표현을 통해 NFA -> DFA를 거치는 Lexical Analysys을 알아보았다. 이제 Syntax Analysis(구문분석)로 넘어간다. 그런데 '사용자가 넣는 모든 입력들을 Syntax Analysis를 처리할 수 있느냐' 이다. 이 궁금증을 짚고 넘어가자.
예를 들어, brace {()} 의 구문일때, 정규표현으로 뽑을 수 있는 경우의 수는 (() , ((((((), ())))))) ... 등이 있을텐데 이것이 정의되기 위해서는 '(' 과 ')'의 갯수가 같아야한다. 즉, 정규표현으로 표현할 수 있는 언어인 Regular Language는 위와 같은 nesting model(중첩 모델)을 표현하기 어렵다. 이를 위해 다른 방식의 grammar가 필요하다.
이를 위해 언어를 표현하는 grammar를 4단계로 나눠서 설명되어져 있다.

여기서 grammar를 설명하기 위해 Terminal과 Non Terminal 에 대한 이해가 필요하다.
Terminal은 grammar에 종속되는 Symbol을 뜻하고 Non Terminal은 규칙을 선택하고 위치에 상관없이 바꿀 수 있는 요소이다.
컴파일러에서는 Terminal Symbol을 Token이라고도 한다. 어떤 input을 넣으면 그에 대한 Token을 찾아주는 프로세스가 Syntax Analysis를 표현하는것이라 할 수 있다.
Context Free Grammar 는 이런 Terminal과 Non-Terminal 의 상관관계를 표현한 문법중 하나이다. CFG의 원록적인 rule이 존재하며 다음의 요소들로 구성되어 있다.
Context Free Grammar G = < Terminal, Non-Terminal, Production, Start Symblo >
시작은 Non-Terminal로 시작해야 하고, 이 Non-Terminal 로부터 파생될 수 있는 Symbol은 Terminal과 Non-Terminal, 그리고 Empty String 등이 있다. 이것이 Production rule이고 수식은 아래와 같다.

예를 들어보자. S -> (S) , S -> ϵ 와 같은 구문이 있다.
CFG에 맞추면 Non-terminal이 시작 심볼이므로 Non-terminal N = {S}
(S) 는 (,S,)로 나눠질 수 있다. 이중 S가 Non-Terminal이므로 그에 따라서 결정되는 (,S,)는 Terminal이다.
Terminal T = { ( , ) } S는 최종적으로 ϵ 으로 도착하기에 Non-Terminal을 찾아낼 여지가 없다.
Production을 구하자면 P = { S -> (S), S-> ϵ} 이 된다.
이를 통해, CFG의 과정은 NonTerminal Symbol이 있는지를 가린 후에 Non-Terminal이 있으면 Rule에 따라 왼쪽에 두고 계속 같은 과정을 수행하는 것이다. 그래서 Non-Terminal이 없을 때까지 수행하다보면 우리가 정규 표현으로 찾을 수 없던 중첩 모델 같은것도 찾아낼 수 있다.

위 예를 표현한 것이다. ϵ은 비어있는 것이다. 결국 최종적으로 S -> ((()))라는 것까지 뽑아낼 수 있다.
Terminal과 Non-Terminal을 구분하기 위해 기본적으로 제공하는 Notational Convention(표기법)이 있다.
Terminal : a, b, c, +, -, ... 0, 1, 2, ... , if, else -> 알파벳 소문자, 연산자, digit, bold string
Non-Terminal : A, B, C, S, expression, term -> 알파벳 대문자, lowercase, italic names
CFG의 기본적인 규칙은 좌측항에 항상 Non-Terminal이 들어와야 하는 것인데, 우측항이 Terminal과 Non-Terminal의 결합 형태로 들어올 수 있다. CFG의 최종 목적은 Non-Termianl이 없을때까지 계속 Production을 적용하는 것이다. 그래서 사전에 정의된 문법을 이용해 Replacement(바꾸는것)를 해야하는데 이 과정을 Derivation(유도)이라고 한다. 아래의 예를 보자
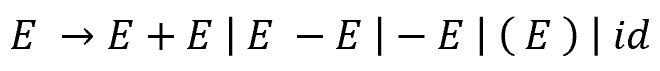
E에 대한 Production set은 E+E, E-E, -E, (E), id 가 있다. 여기서 E->(id) 라는 새로운 문법이 성립하는지를 알고싶다면 앞의 Derivation을 적용하면 된다. 아래와 같다.

이같은 과정을 -(id)에 대한 '유도' 라 하며 이를통해, -(id) 가 문법에 충족된다고 말할 수 있다. 여기서 사전에 정의된 문법을 이용해 유도가 가능한 경우에는 보통 Derives in zero or more steps 이라 하는데 표현은 A=>*a 라 하고 위와 같이 replacement를 통해 문법을 찾는 경우는 Derives in one more steps 라 하고 A=>+a 라고 사용한다. 위 예에서는 E=>+-(id) 라고 표현할 수 있다.
이 예제를 트리로 표현할 수도 있다.

위의 예제는 간단해서 쉽게 유도할 수 있지만 만약, E-> id+id*id 라는 문법을 적용하면 복잡해질 수 있다. 이때부턴 어떤 요소부터 유도를 수행하느냐에 따라 결과가 다르다. 이러한 현상을 CFG의 Ambiguty라 하며 이 유도를 어떤 방향으로 수행할 것인지 규칙을 정해야한다. 보통 좌측 유도와 우측 유도를 사용하며 트리의 모양은 아래와 같이 된다. 이번 예제는 출처의 그림을 그대로 사용한다.

위의 예제는 규칙을 정해주기 전까지 맞다 틀리다를 결정할 수 없다. 우리가 Compiler를 만든는데 있어 사용하려던 Automation의 개념과 의미가 모호성에 대해 grammar가 매우 복잡해 질수있다. 결국 몇몇 케이스에 대해서만 정의하고 그 외 치명적이지 않은 모호성에 대해서는 허용할 수 밖에 없다. 이를 위해 추가적인 정보가 더 필요하며 위의 예에서는 사칙연산에 대한 규칙이 더 필요하다. 대부분의 언어에 적용되어 있는 규칙에 따라 위의 예를 해결해본다.
E->id+id*id 라는 문법을 얻었으며 그 시작을 E라는 Non-Terminal로부터 출발해서 위에서 아래로 분리하는 Top-Down 을 사용한다. 이 과정에서 왼쪽에서부터 자기자신이 하나하나씩 E가 id로 replacement 된다.
이러한 방식을 보통 Left-Recursive Grammar 라고 한다.
이 방식은 Top-down에서 문제를 일으킨다. Recursion 수가 끝없이 증가하는 경우가 발생한다. 예를들어,ㅣ
E -> E + T | id
=> E -> E + T -> E + T + T -> E + T + T + T + T -> ....
이같이 대체하다가 시작점이 어디서부터인지를 가늠할 수 없게된다. 그래서 최대한 분해를 할때는 이 Left Recursine된 Production을 제거해줘야 한다. 이를 위해 Prime이라는 것을 사용하고 최대한 자기자신이 Recursion되지 않게 grammar를 rewrite해준다.

원래의 문법에 자기자신이 포함된 형태가 포함되어 이를 제거해주기 위해 A'을 삽입하고 이에대한 문법을 따로 정의해준 것이다. 이 방식을 사용하여 그냥 α나 Empty String이 나오면 Terminal이 나오면 Terminal이 된다. 이렇게 해주는 과정을 Left Factoring 이라 한다.
'컴파일러_Compiler' 카테고리의 다른 글
| [Compiler] EBNF_Extended Backus-Naur Form (0) | 2019.09.11 |
|---|---|
| [Compiler] DFA -> Minimal DFA : State Minimization Algorithm (0) | 2019.07.22 |
| [Compiler]NFA -> DFA : Subset Construction Algorithm (0) | 2019.07.07 |
| [Compiler]TCA(Thompson's Construction Algorithm) (0) | 2019.07.07 |
| [Compiler] NFA/DFA (0) | 2019.06.23 |